This page was generated by nbsphinx from docs/notebooks/analysis/swept_langmuir/find_floating_potential.ipynb.
Interactive online version: .

Swept Langmuir Analysis: Floating Potential

This notebook covers the use of the find_floating_potential() function and how it is used to determine the floating potential from a swept Langmuir trace.

The floating potential, \(V_f\), is defined as the probe bias voltage at which there is no net collected current, \(I=0\). This occurs because the floating potential slows the collected electrons and accelerates the collected ions to a point where the electron- and ion-currents balance each other out.

%matplotlib inline

import matplotlib.pyplot as plt
import numpy as np
import pprint

from pathlib import Path

from plasmapy.analysis import swept_langmuir as sla

plt.rcParams["figure.figsize"] = [10.5, 0.56 * 10.5]

np.set_printoptions(precision=4, threshold=16)

Contents:

1. How find_floating_potential() works

   1. Notes about usage

   2. Knobs to turn

2. Calculate the Floating Potential

   1. Interpreting results

   2. Plotting results

How find_floating_potential() works

1. The passed current array is scanned for points that equal zero and point-pairs that straddle where the current, \(I\), equals zero. This forms an collection of “crossing-points.”

2. The crossing-points are then grouped into “crossing-islands” based on the threshold keyword.

   • A new island is formed when a successive crossing-point is more (index) steps away from the previous crossing-point than defined by threshold. For example, if threshold=4 then a new island is formed if a crossing-point candidate is more than 4 steps away from the previous candidate.

   • If multiple crossing-islands are identified, then the function will compare the total span of all crossing-islands to min_points. If the span is greater than min_points, then the function is incapable of identifying \(V_f\) and will return numpy.nan values; otherwise, the span will form one larger crossing-island.

3. To calculate the floating potential…

   • If the number of points that make up the crossing-island is less than min_points, then each side of the “crossing-island” is equally padded with the nearest neighbor points until min_points is satisfied.

   • If fit_type="linear", then a scipy.stats.linregress fit is applied to the points that make up the crossing-island.

   • If fit_type="exponential", then a scipy.optimize.curve_fit fit is applied to the points that make up the crossing-island.

Notes about usage

• The function provides no signal processing. If needed, the user must smooth, sort, crop, or process the arrays before passing them to the function.

• The function requires the voltage array to be monotonically increasing.

• If the total range spanned by all crossing-islands is less than or equal to min_points, then threshold is ignored and all crossing-islands are grouped into one island.

Knobs to turn

• fit_type

  There are two types of curves that can be fitted to the identified crossing point data: "linear" and "exponential". The former will fit a line to the data, whereas, the latter will fit an exponential curve with an offset. The default curve is "exponential" since swept Langmuir data is not typically linear as it passes through \(I=0\).

• min_points

  This variable specifies the minimum number of points that will be used in the curve fitting. As mentioned above, the crossing-islands are identified and then padded until min_points is satisfied. Usage:

  • min_points = None (DEFAULT): min_points is chosen to be the larger of 5 or factor * array_size, where factor = 0.1 for "linear" and 0.2 for "exponential".

  • min_points = numpy.inf: The entire array is fitted.

  • min_points is an integer >= 1: min_points is the minimum number of points to be used.

  • 0 < min_points < 1: The minimum number of points is taken as min_points * array_size.

• threshold

  The max allowed index distance between crossing-points before a new crossing-island is formed.

Calculate the Floating Potential

Below we’ll compute the floating potential using the default fitting behavior (fit_type="exponential") and a linear fit (fit_type="linear").

# load data
filename = "Beckers2017_noisy.npy"
filepath = (Path.cwd() / ".." / ".." / "langmuir_samples" / filename).resolve()
voltage, current = np.load(filepath)

# voltage array needs to be monotonically increasing/decreasing
isort = np.argsort(voltage)
voltage = voltage[isort]
current = current[isort]

# get default fit results (exponential fit)
results = sla.find_floating_potential(voltage, current, min_points=0.3)

# get linear fit results
results_lin = sla.find_floating_potential(voltage, current, fit_type="linear")

Interpreting results

The find_floating_potential() function returns a 2 element tuple, where the first element is the calculated floating potential \(V_f\) and the second element is a named tuple VFExtras containing additional parameters resulting from the calculation.

• results[0] is the determined floating potential (same units as the pass voltage array)

vf = results[0]
vf

-5.665730698520963

• results[1] is an instance of VFExtras and contains additional information from the calculation

extras = results[1]
extras

VFExtras(vf_err=0.45174119664601947, rsq=0.9564766142727993, fitted_func=f(x) = a exp(alpha x) + b <class 'plasmapy.analysis.fit_functions.ExponentialPlusOffset'>, islands=[slice(192, 195, None), slice(201, 210, None)], fitted_indices=slice(155, 247, None))

• extras[0] = extras.vf_err = the associated uncertainty in the \(V_f\) calculation (same units as vf)

(extras[0], extras.vf_err)

(0.45174119664601947, 0.45174119664601947)

• extras[1] = extras.rsq = the coefficient of determination (r-squared) value of the fit

(extras[1], extras.rsq)

(0.9564766142727993, 0.9564766142727993)

• extras[2] = extras.fitted_func = the resulting fitted function

  • extras.fitted_func is a callable representation of the fitted function I = extras.fitted_func(V).

  • extras.fitted_func is an instance of a sub-class of AbstractFitFunction. (FitFunction classes)

  • Since extras.fitted_func is a class instance, there are many other attributes available. For example,

    • extras.fitted_func.params is a named tuple of the fitted parameters

    • extras.fitted_func.param_errors is a named tuple of the fitted parameter errors

    • extras.fitted_func.root_solve() finds the roots of the fitted function. This is how \(V_f\) is calculated.

(
    extras[2],
    extras.fitted_func,
    extras.fitted_func.params,
    extras.fitted_func.params.a,
    extras.fitted_func.param_errors,
    extras.fitted_func.param_errors.a,
    extras.fitted_func(vf),
)

(f(x) = a exp(alpha x) + b <class 'plasmapy.analysis.fit_functions.ExponentialPlusOffset'>,
 f(x) = a exp(alpha x) + b <class 'plasmapy.analysis.fit_functions.ExponentialPlusOffset'>,
 FitParamTuple(a=0.010275375458525872, alpha=0.338277953104458, b=-0.0015115846190350466),
 0.010275375458525872,
 FitParamTuple(a=0.00031439926674768734, alpha=0.02163110937712501, b=0.00012999596409070833),
 0.00031439926674768734,
 0.0)

• extras[3] = extras.islands = a list of slice objects representing all the identified crossing-islands

(
    extras[3],
    extras.islands,
    voltage[extras.islands[0]],
)

([slice(192, 195, None), slice(201, 210, None)],
 [slice(192, 195, None), slice(201, 210, None)],
 array([-7.496 , -7.2238, -7.1512]))

• extras[4] = extras.fitted_indices = a slice object representing the indices used in the fit

(
    extras[4],
    extras.fitted_indices,
    voltage[extras.fitted_indices],
)

(slice(155, 247, None),
 slice(155, 247, None),
 array([-11.6594, -11.6488, -11.5358, ...,  -1.251 ,  -0.9812,  -0.8504]))

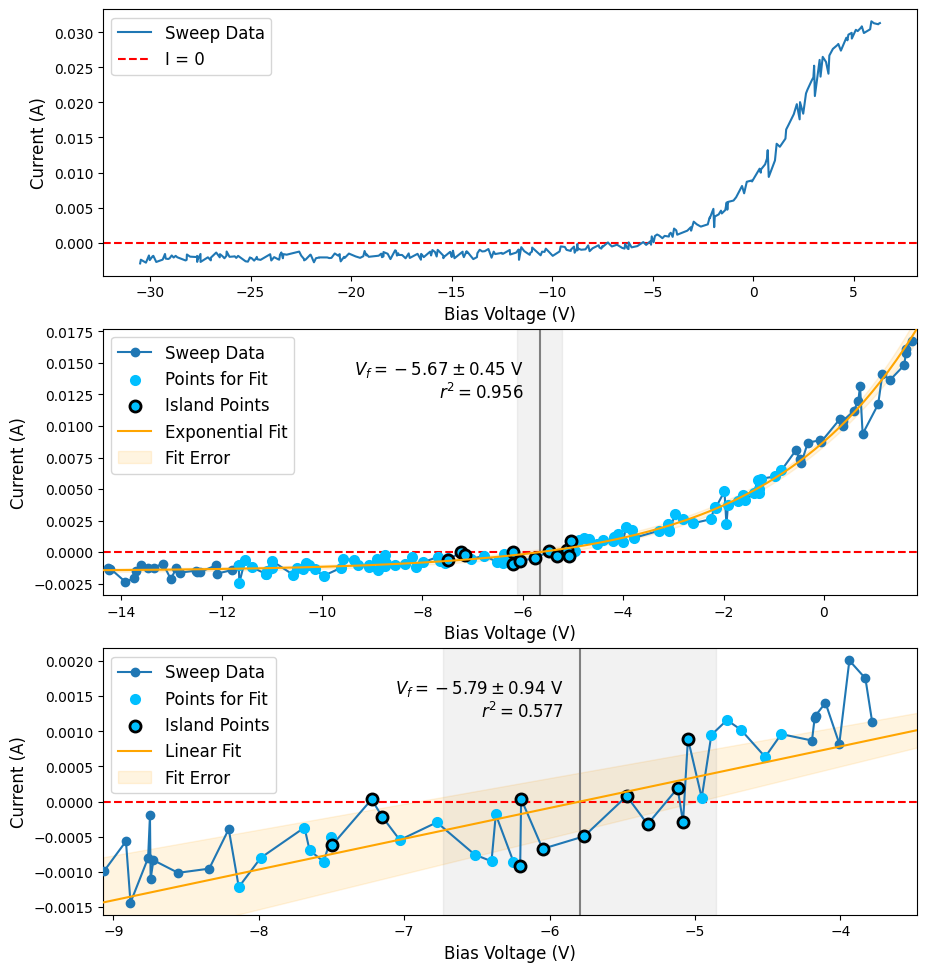
Plotting results

figwidth, figheight = plt.rcParams["figure.figsize"]
figheight = 2.0 * figheight
fig, axs = plt.subplots(3, 1, figsize=[figwidth, figheight])

# plot original data
axs[0].set_xlabel("Bias Voltage (V)", fontsize=12)
axs[0].set_ylabel("Current (A)", fontsize=12)

axs[0].plot(voltage, current, zorder=10, label="Sweep Data")
axs[0].axhline(0.0, color="r", linestyle="--", label="I = 0")
axs[0].legend(fontsize=12)

# zoom on fit
for ii, label, rtn in zip([1, 2], ["Exponential", "Linear"], [results, results_lin]):
    vf = rtn[0]
    extras = rtn[1]

    # calc island points
    isl_pts = np.array([], dtype=np.int64)
    for isl in extras.islands:
        isl_pts = np.concatenate((isl_pts, np.r_[isl]))

    # calc xrange for plot
    xlim = [voltage[extras.fitted_indices].min(), voltage[extras.fitted_indices].max()]
    vpad = 0.25 * (xlim[1] - xlim[0])
    xlim = [xlim[0] - vpad, xlim[1] + vpad]

    # calc data points for fit curve
    mask1 = np.where(voltage >= xlim[0], True, False)
    mask2 = np.where(voltage <= xlim[1], True, False)
    mask = np.logical_and(mask1, mask2)
    vfit = np.linspace(xlim[0], xlim[1], 201, endpoint=True)
    ifit, ifit_err = extras.fitted_func(vfit, reterr=True)

    axs[ii].set_xlabel("Bias Voltage (V)", fontsize=12)
    axs[ii].set_ylabel("Current (A)", fontsize=12)
    axs[ii].set_xlim(xlim)

    axs[ii].plot(
        voltage[mask],
        current[mask],
        marker="o",
        zorder=10,
        label="Sweep Data",
    )
    axs[ii].scatter(
        voltage[extras.fitted_indices],
        current[extras.fitted_indices],
        linewidth=2,
        s=6**2,
        facecolors="deepskyblue",
        edgecolors="deepskyblue",
        zorder=11,
        label="Points for Fit",
    )
    axs[ii].scatter(
        voltage[isl_pts],
        current[isl_pts],
        linewidth=2,
        s=8**2,
        facecolors="deepskyblue",
        edgecolors="black",
        zorder=12,
        label="Island Points",
    )
    axs[ii].autoscale(False)
    axs[ii].plot(vfit, ifit, color="orange", zorder=13, label=label + " Fit")
    axs[ii].fill_between(
        vfit,
        ifit + ifit_err,
        ifit - ifit_err,
        color="orange",
        alpha=0.12,
        zorder=0,
        label="Fit Error",
    )
    axs[ii].axhline(0.0, color="r", linestyle="--")
    axs[ii].fill_between(
        [vf - extras.vf_err, vf + extras.vf_err],
        axs[1].get_ylim()[0],
        axs[1].get_ylim()[1],
        color="grey",
        alpha=0.1,
    )
    axs[ii].axvline(vf, color="grey")
    axs[ii].legend(fontsize=12)

    # add text
    rsq = extras.rsq
    txt = f"$V_f = {vf:.2f} \\pm {extras.vf_err:.2f}$ V\n"
    txt += f"$r^2 = {rsq:.3f}$"
    txt_loc = [vf, axs[ii].get_ylim()[1]]
    txt_loc = axs[ii].transData.transform(txt_loc)
    txt_loc = axs[ii].transAxes.inverted().transform(txt_loc)
    txt_loc[0] -= 0.02
    txt_loc[1] -= 0.26
    axs[ii].text(
        txt_loc[0],
        txt_loc[1],
        txt,
        fontsize="large",
        transform=axs[ii].transAxes,
        ha="right",
    )